CoursePlan Requirement Checking Design Document
by Sam Zhou
Background#
Before we use graphs to compute and represent the status of requirement fulfillment, we compute them in a quite naive way. We have a big json that contains the mapping from requirement to course list. i.e. given a requirement, you can use the information from the big json to tell which classes can be used to satisfy it or its sub-requirements. Such setup can work in most of the cases. However, it makes certain problems more painful. The most important example is double counting detection/elimination. The real-life example is the MATH 4710 class. It can be used to satisfy multiple things at once: engineering probability, engineering substitution for a CHEM class, or as one of your external spec. However, the engineering double counting rules says that you can double count it for probability, but not both for CHEM replacement or external spec. The current mapping setup makes it both harder and computationally more expensive (O(n^2) instead of O(n)) to detect these bad double counting. At the same time, it’s also not a good idea to only map from courses to requirements, because that will make computing requirement fulfillment statistics harder.
Why Graph Is the Best Abstraction#
From the above section, we can find that we need some abstraction that allows us to look at the requirement fulfillment picture in both ways. For example, we should be able to easily find all courses that satisfy one requirement, or all requirements that a course can potentially be used to satisfy.
Graph is the only elementary data structure that can provide O(1) access for these operations. More specifically, the graph is a bipartite graph, with requirements on one side and courses on the other side. We can achieve optimal space efficiency by using two HashTables to encode the graph: one is a map from requirements to course lists, and the other is a map from course to requirement list. We can create a class that is composed of the two maps and ensures that they are in sync with each other.
It’s worth noting that this bipartite graph should be the most powerful abstraction we need for representing requirement fulfillment. No matter how crazy Cornell is when deciding graduation requirement, we will always have a list of requirements and a list of courses to deal with, and the bipartite graph has the expressive power to encode all 2^(m*n) possible relations between two lists.
Main Requirement Checking Steps#
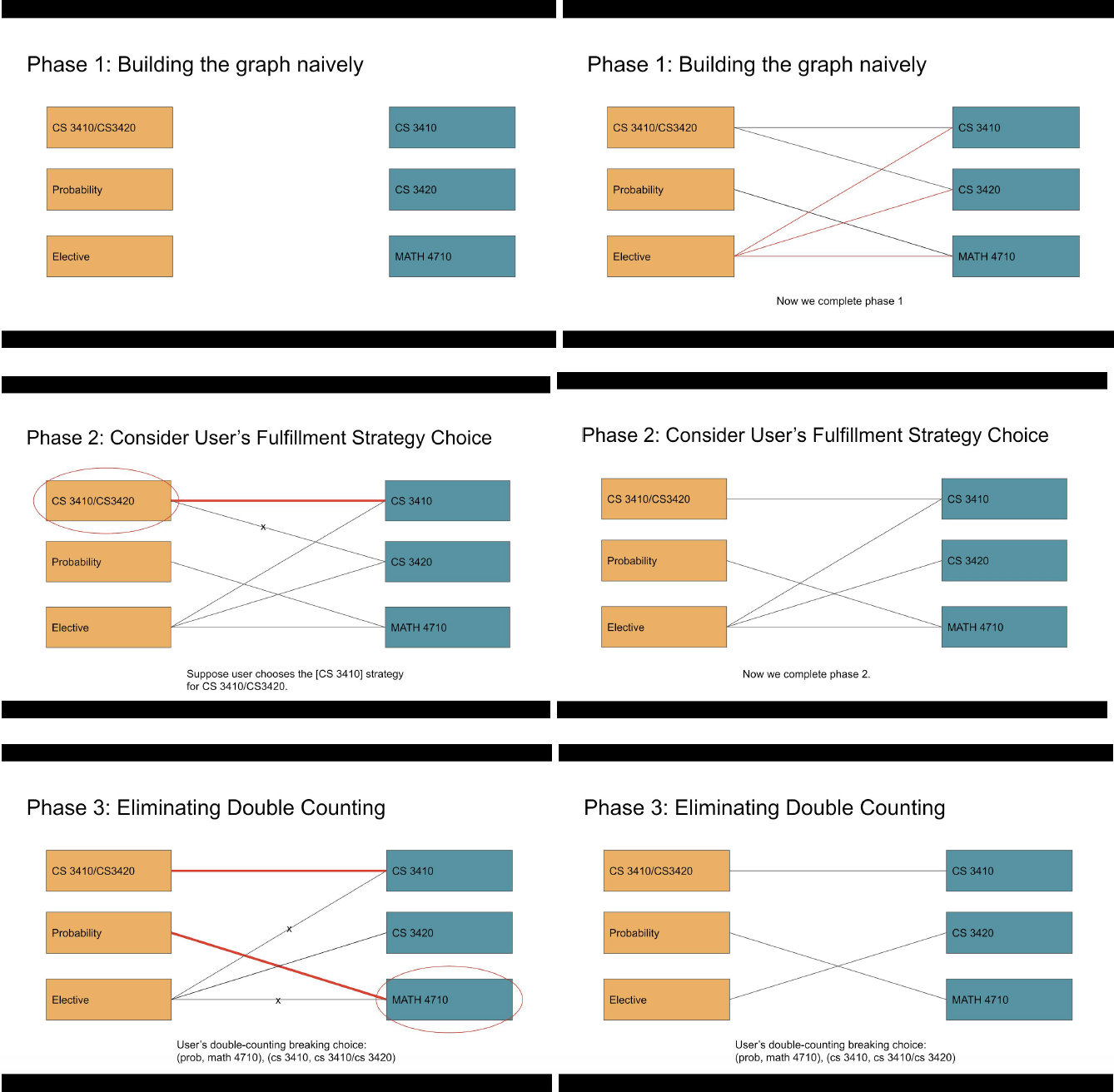
The core of the requirement checking steps are follows:
- Building a rough graph. In this step, we connect requirement r and course c whenever we find that c is in the course list of r in the big requirement json.
- Some requirements might have multiple fulfillment options and the user may choose one of them. Remove all the edges from requirements to courses that are not part of the user’s choice.
- The user might make some choices on tie-breaking for double-counted courses. Remove all the edges from courses to requirements that are not the picked requirement in the choice.
The following screenshots show an example walkthrough of the steps:
Implementation Guides for Various Features#
The main algorithm provides only a simplified picture on how we can check requirement fulfillment. There are still some implementation details that need to be figured out to account for all real world usage instead of pure math. Also, we need to account for all other required features (e.g. AP/IB credits) that seems not to be part of the graph.
In Java, every object has equals() and hashCode() method which makes hash table
implementation easy. However, the JS Map object can only reliably work if you use string or
number as its key. Therefore, in order for the Map<Requirement, Course[]> to work, we
must turn each requirement into a string that can uniquely identify itself. Same is true for
courses.
Since we directly maintain the requirement data by ourselves, we can give each requirement a
unique identifier. We can use the semester ID and the course ID from the course roster to
uniquely identify a course. Then for the hash table, we can give it an additional function
getUniqueHash that takes a requirement/course and turns it into a string to be used for key.
With this setup, the map for the final example graph would look like:
AP/IB/Transfer Credits#
We can use the equality notation setup in the last section to easily achieve accounting for the credits. Every AP/IB test or transfer course is designed to be a replacement for some class. Therefore, we can give it the same ID as the course it will replace. For example, we can give AP CS the same ID as the CS 1110, so that AP CS will be a fake course that looks like:
while the CS 1110 object might look like
Double Counting Detection#
To detect illegally double-counted courses, we can linearly scan through every course. For every course, we find all requirements that are connected to it. For those connected requirements, we filter away all requirements that allow double counting (e.g. engineering probability). Then if the leftover list has length >= 2, we know that the course is illegally double-counted.
Potential Concerns#
The current code is not written in a way that expects to get a graph for requirement fulfillment. Therefore, we have to write additional adapter code to transform the graph structure into the flattened list to make it work with the old code in the short term. However, given the powerful abstraction and ease of feature implementation the graph can provide, this is a painful but the correct migration to do.
We also currently have an outstanding PR on toggleable requirements that was created before I introduced this new setup, so we also have to rework on that PR so make it integrated to the rest of the system.